Grover's Algorithm

Previous Index Next

The Actual Algorithm

Here we go through the basic steps of the algorithm and explain how they can be implemented as a simple quantum circuit.

Outline
Implementing as a Quantum Circuit

The Oracle
The Diffusion Operator
Full Quantum Circuit
Example Circuit in Quirk

Outline

Here we will quickly describe Grover’s algorithm in a high-level way.

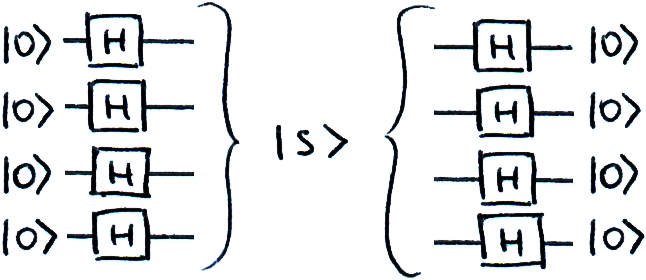
The first step of the algorithm is to initialise the starting state |s⟩, a superposition of all possible inputs. We know this can be easily accomplished using a Hadamard transform on each qubit.

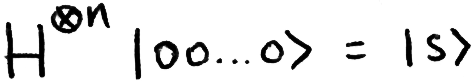
The intital state is an equal superposition of all measureable inputs, and is easily constructed from Hadamard transforms.

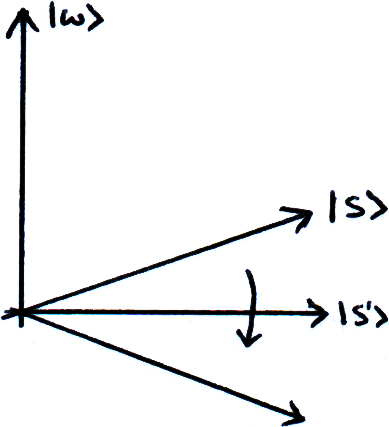
Since we want our algorithm to output ω, we want our qubits to be as close to the state |ω⟩ as possible when we measure them. The algorithm is tasked with moving the state of the qubits from |s⟩ to |ω⟩. To simplify, we can split every state in our computation into one of two categories: |ω⟩ and not |ω⟩. Since we only care about |ω⟩ and all the states that are not |ω⟩, we can plot this on a 2D graph:

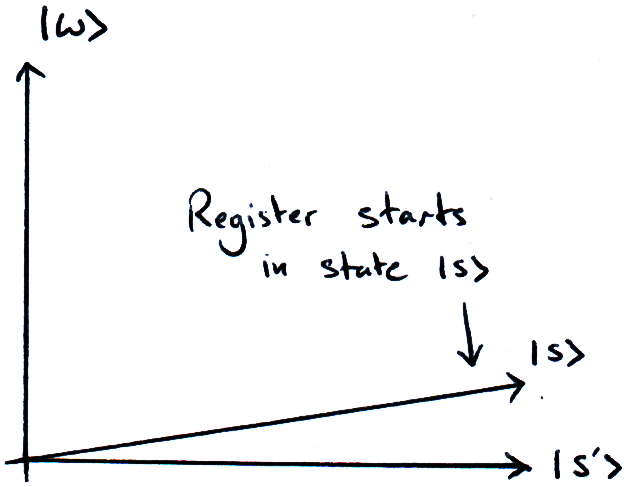
Our qubits start in the state |s⟩, and we are trying to get to |ω⟩

Where |s’⟩ is the equal superposition of all states excluding |ω⟩. This means |s’⟩ is perpendicular to |ω⟩. Our computer is never actually in the state |s’⟩ (if it is then we’re doing something very wrong!), we just use |s’⟩ to act as the axis on our graph, and to illustrate the reflections we are doing.

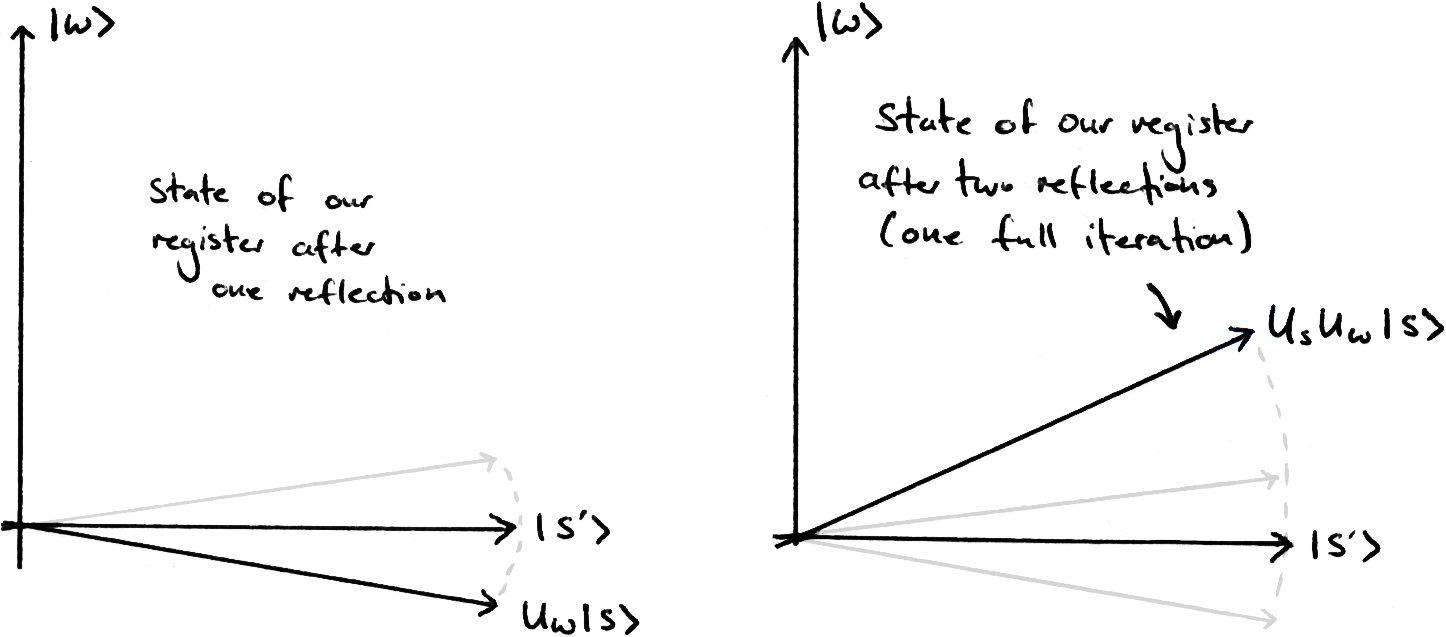
We perform a reflection around |s’⟩ (this operator is called ‘U_ω’) and a reflection around |s⟩ (called ‘U_s’), and repeat until we are close to |ω⟩. This takes ~2^n/2 repetitions.

The first step of Grover's algorithm is to give a negative phase to the |ω⟩ component of |s⟩, this corresponds to a reflection through |s'⟩. The second step is to perform a reflection through |s⟩

Implementing Grover's Algorithm as a Quantum Circuit

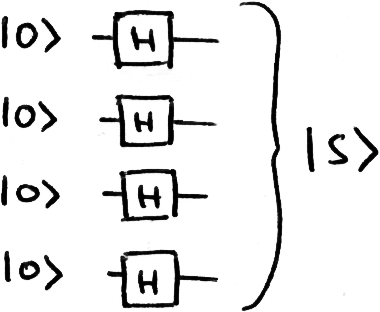
Here we will go through each step and show how they can be performed by a universal quantum computer. The first step, initialising the state |s⟩ is very simple: We do a Hadamard transform (H-gate) on each qubit, this gives us a uniform superposition of every state.

We need to set up our initial superposition, |s⟩. To do this we apply a H-gate to each qubit

The Quantum Oracle

(A very cool title)

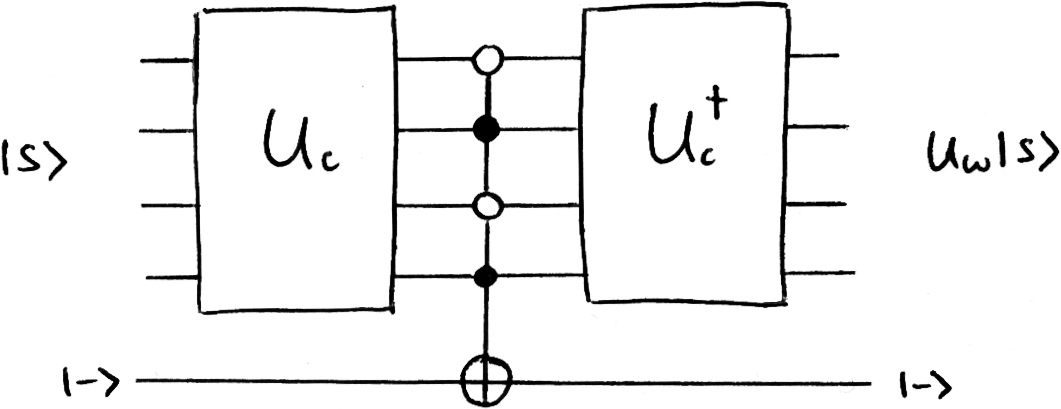
The second operation, the reflection around |s’⟩ is the most interesting step, this is where our query circuit comes in. To perform the reflection, we need a circuit that adds a negative phase to the |ω⟩ component of our vector.

The first step of Grover's algorithm is to give a negative phase to the |ω⟩ component of |s⟩, this corresponds to a reflection through |s'⟩

Firstly, we implement our classical query circuit as a quantum circuit, (how we actually do this depends on the problem and we will cover this later,) this means we can pass it our superposition of inputs to get a new equal superposition of output states.

We then use our checker circuit to add a negative phase to the state we’re searching for. In the image below, our |ω⟩ is the state |0101⟩. This is easy enough to check for, we just use a Toffoli gate with the appropriate controls.

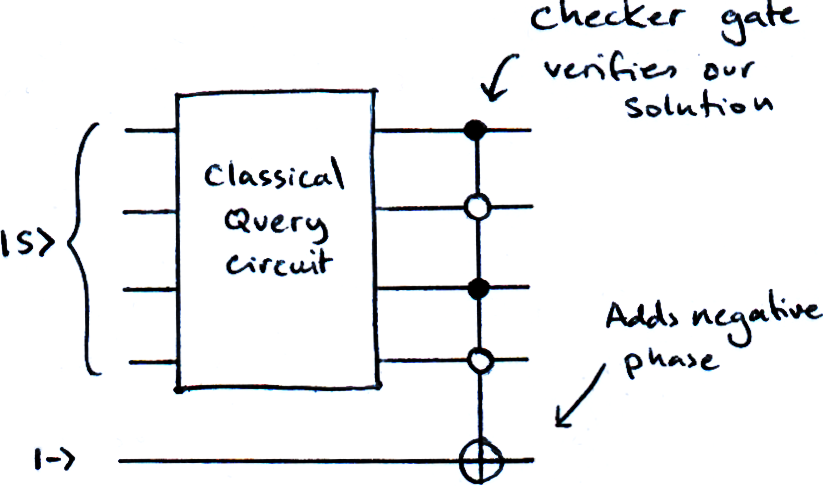
We pass |s⟩ through our classical query circuit, and use our checker circuit to invert the phase of our solution

But how do we apply the negative phase? Remember that if we apply an X-gate to a qubit in the |-⟩ state, we get back a qubit in the state -|-⟩:

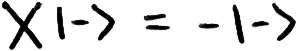
Applying an X-gate to a qubit in the state |-⟩ inverts its phase

So we use our checker circuit to apply an X-gate to a |-⟩ qubit. We then reverse the classical query circuit to get back our initial |s⟩, except the |ω⟩ component is negative.

We describe the combined state of the search qubits and the |-⟩ qubit using the Kronecker product (link to section). This explains how the negative phase introduced with the checker circuit applies to the whole state:

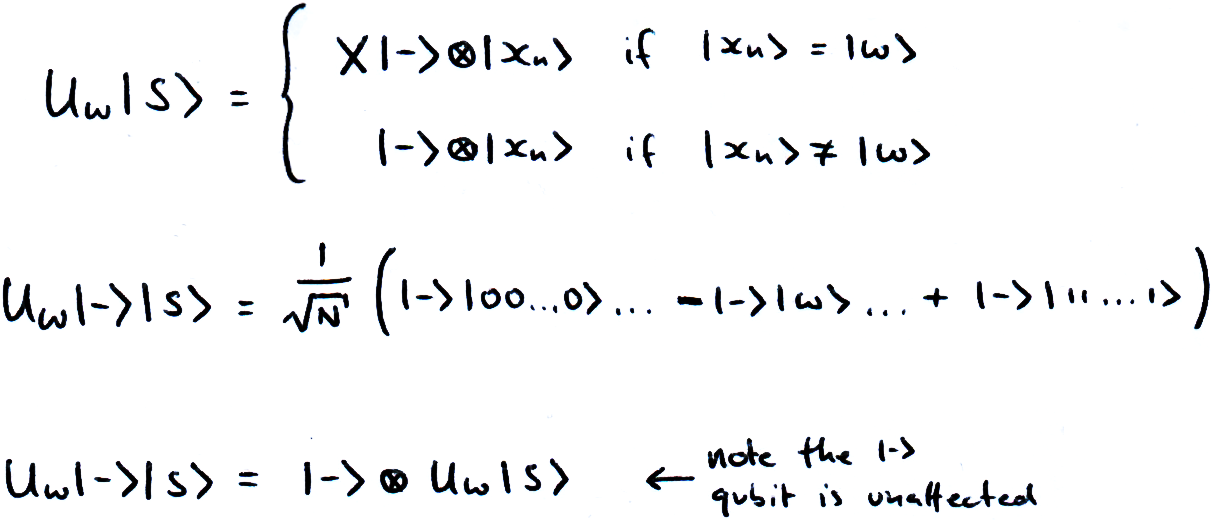
The X-gate is only applied to the |-⟩ qubit if our register's state is |ω⟩, therefore a negative phase is only applied to the state |ω⟩

And remember that any states that are not |ω⟩ will not activate the checker circuit and will pass through unaffected. This whole circuit is a functioning oracle, it performs a reflection about |s’⟩ as specified in Grover’s algorithm.

A full oracle constructed from a classical query circuit (Uc)

The Diffusion Operator

The next step is the reflection through |s⟩, this step is actually really simple, and is the same for every database search. This reflection is called the ‘Diffusion Operator’. To perform the diffusion operator we need to invert anything perpendicular to |s⟩, and we do this following a similar method to the Oracle.

We will do the transformation that turns |s⟩ into the all-zeroes vector |000..0⟩, and invert anything that is not |000..0⟩, before transforming back again. Before, we easily created |s⟩ by applying a H-gate to each qubit, if we want to go back the all-zeroes vector we just apply a H-gate to each qubit again.

Transforming the all-zeroes state |0000⟩ to the equal superposition state |s⟩ and back.

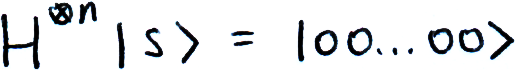
The whole diffusion operator looks like this:

Note that we have applied a negative phase to all the states that are parallel to |s⟩, not perpendicular as we specified. Since global phase can be ignored , this is completely equivalent. We now have all the steps required to complete Grover’s algorithm.

As a full Quantum Circuit

We can combine our classical query circuit, checker circuit and diffusion operator to complete the first iteration of Grover’s algorithm:

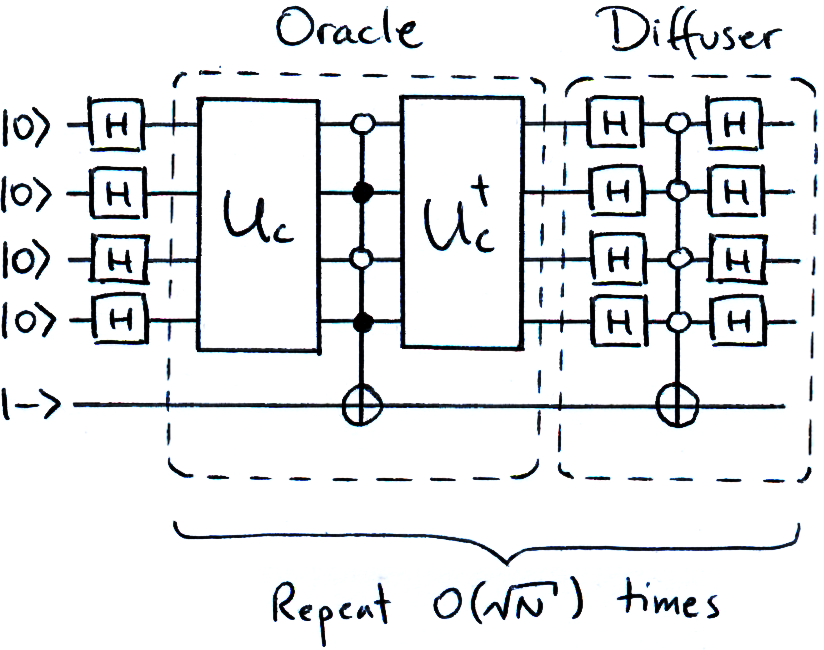
Simple! We then repeat the oracle and diffuser O(√N) times.

Example Circuit in Quirk

Here is an example circuit in Quirk

Grover's Algorithm on 4 Qubits

The bottom 4 qubits are the work qubits, which output the answer. The qubit above the work qubits is the |-⟩ qubit we use to add the negative phase, and the top qubit is used for labels. In this demonstration we have no classical query circuit (U_c), we will create a query circuit and use it in the next section.

Our algorithm searches for |0101⟩. Watch how the probability of measuring |0101⟩ grows with each iteration, and reaches 90.8% chance after two iterations. Classically (with random guessing) we would have a ~13% chance of getting |0101⟩ after two guesses.