Grover's Algorithm
Using Grover's Algorithm
An Example
In this section we give an example of using Grover’s algorithm (quantum search) to solve a computational problem. This should hopefully help the reader understand how we can turn our oracle into a usable quantum circuit.
Contents
Computational Search
Until now we have described our oracle as querying a database. While we could in theory use a real database, such as phonebook, we would need to query it in superposition which would require specialised hardware which is beyond the scope of this site. Instead we will apply quantum search to computational problems.
Say we have a function:
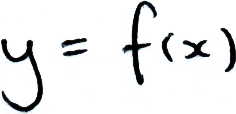
And we want to find the value of x that gives a desired value of y, a solution to this problem is to use computational search; we search through all the possible values of x until we output y.
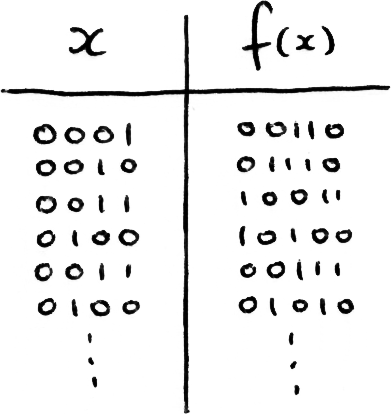
This still behaves as a database search, the difference is that instead of querying an external database, we can do the computation f(x) right on our computer. An example of computational search could be path finding, where we try different paths and calculate their length until we find a sufficiently short one, or solving sudoku puzzles by trying random combinations of variables until we find a solution.
Note that both these problems have structure that can be exploited, if you have ever tried a sudoku you will know that there are much cleverer ways to solve it than random guessing, and that these methods are much quicker! We will discuss exploiting structure in a later section
NP- Complete Problems
NP-complete problems are problems in which it is easy (polynomial time) to verify a solution, but difficult (exponential time, as far as we know) to find the solution. NP-complete problems are very important in computer science; you may have heard of P vs NP - this is a famous unsolved problem that asks whether a polynomial-time solution to NP-complete problems exists.
Using the example of a Sudoku: If you were given the solution to a Sudoku you could verify it very quickly, possibly in under a minute, but finding the answer to a Sudoku normally takes a lot longer.
Algorithms for solving NP-complete problems often involve some kind of computational search which makes them a great potential application for our quantum search.
SAT Problems
We now introduce Boolean Satisfiability (SAT) as an example of a real computational problem that can be solved using quantum search.
Background
We will use Grover’s algorithm to solve SAT problems, a specific NP-complete problem. There is no known algorithm that solves an NP-complete problem in less than exponential time, but a solution can be verified in polynomial time.
SAT was the first problem proven to be NP-complete, and due to this has been widely studied. SAT is not only useful for purely mathematical uses; encryption algorithms such as the Data Encryption Standard can be reduced to 3-SAT and SAT solvers can be used in protein design and circuit synthesis.
What is a SAT Problem?
SAT is short for Boolean Satisfiability.
A SAT problem takes n variables which can be assigned either ‘True’ or ‘False’ (in our computer, our qubits are our variables, we use |1⟩ to represent ‘True’ and |0⟩ to represent ‘False’).
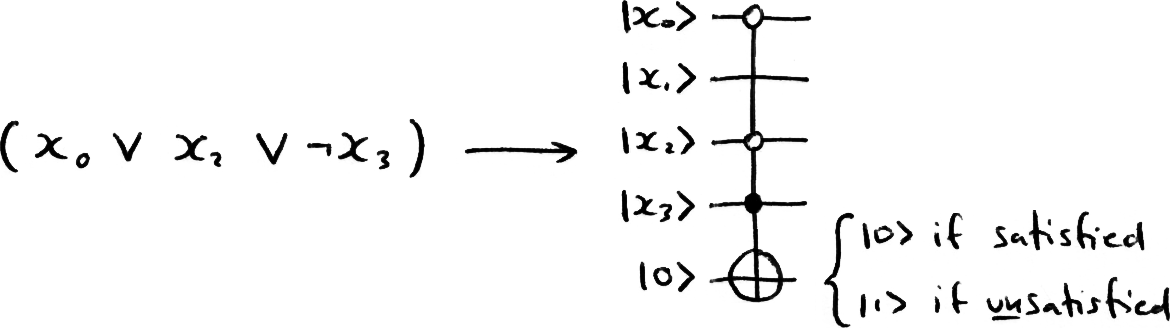
A clause is a collection of literals, and a literal describes the assignment of a specific variable. For example the clause given below has three literals (the ¬ indicates a false literal, the ∨ is the Boolean ‘OR’ and demands that at least one clause must be satisfied):
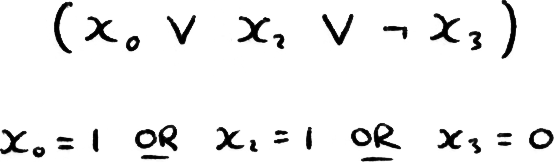
So the only state that satisfies this clause has:
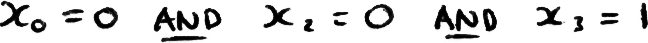
If at least one of these criteria are met, the clause is satisfied, so each clause can be seen as ruling out specific combinations of variable assignments. A solution is an assignment of the n variables that satisfies every clause. In a k-SAT problem there are m clauses, with k literals in each clause. The hardest SAT problems have a small (but none zero) number of solutions, these problems generally have a fixed ratio of m to n which depends on k, for 3-SAT this ratio is ∼ 5, so there are approximately 5 clauses per variable in a difficult 3-SAT problem.
We can map each clause in a SAT problem to a k-input Toffoli gate. Since each clause rules out one combination of variables, we can flip a target bit if our clause is unsatisfied:
Building a SAT Oracle
First we need to create our classical SAT query circuit. The simplest way we can do this is to have each clause flip a different ancillary |0⟩ qubit, and our checker circuit only acts if no clauses are unsatisfied. We then reverse our classical query circuit to get a complete oracle:

We now have a circuit that only acts on the |-⟩ qubit if all clauses are satisfied – a functioning oracle! It must be noted that while this circuit works, it uses a large number of ancillary qubits; we discuss how we can optimise our circuits in (link to section).
A Full SAT Solving Circuit
We now have a working oracle, all we need to do is combine it with our diffusion operator and create our starting state, |s⟩:

This example problem has two clauses and two solutions (|001⟩ & |101⟩).
We only needed one iteration to achieve 100% probability of measuring a solution.
Note that this example solves a 2-SAT problem, which is not NP-complete and does have a polynomial time algorithm. This problem was chosen for this example to keep the circuit to 6 qubits and 9 columns, but this exact process can be used to solve 3-SAT & larger problems.
Considerations
This example is intended to:
- Show how quantum search can be useful, and provide some motivation for learning about quantum search.
- Give an example of converting real problems into quantum circuits.
Unfortunately this SAT solver would not be very useful compared to modern classical SAT solvers for a few main reasons:
- We don’t know how many solutions there are to each problem and we risk over-rotating and getting no useful answer at all.
- This search is naïve, or 'brute force' - we don’t exploit any structure.
- The number of ancillary qubits needed is very large (much greater than n).
We will address each of these points and discuss how to overcome them in later section.