Grover's Algorithm
Preamble
This is the first section on Grover's algorithm. It sets up the problem of unstructured computational search in a way that it can be solved using quantum circuits, and provides context for the next section.
Contents
Unstructured Search
A phonebook is an example of a structured database; Since a phonebook is sorted alphabetically, if given a name, we can quickly (in logarithmic time) locate that person’s phone number. Even if the phonebook has a large number of entries we can still find the name we’re looking pretty quickly. We will cover structured search in it’s own dedicated section.
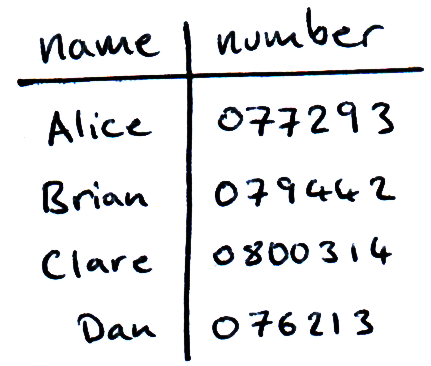
But if we turn the problem around, i.e. we are given a phone number and asked to find it’s corresponding name, the search problem suddenly becomes very difficult. We can make no educated guesses about where the number we’re looking for might be. The best classical algorithm for unstructured search is ‘random guessing’, where we pick out entries at random until we happen upon the phone number we’re looking for. This algorithm grows linearly with the number of entries (N) in the phonebook, since it will take (on average) N/2 queries of the database to find the correct entry.
Thinking about Unstructured Search like a Computer
Since there is absolutely no way to search a real phonebook using Grover’s algorithm, we need to think about database search like a computer scientist. Firstly, to help ease the transition to quantum circuits, we will assume the names and numbers in our phonebook are stored in binary, and we will call them ‘inputs’ and ‘outputs’ respectively. Now note that the number of entries we have in our database (N) is related to the number of bits (n) by N = 2n.
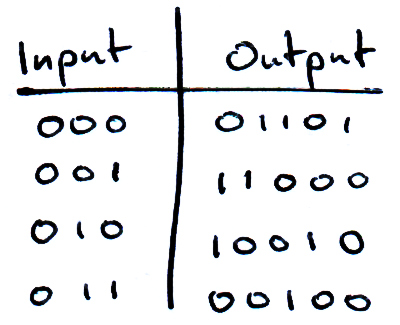
By convention, we call the output we’re looking for ‘ω’.
The Query Circuit
The query circuit is a function that takes an address (the name) as input, and outputs the data at that address (the phone number). At the moment we treat the query circuit as a ‘black box’, which means we do not care about how it works, but we will do later.
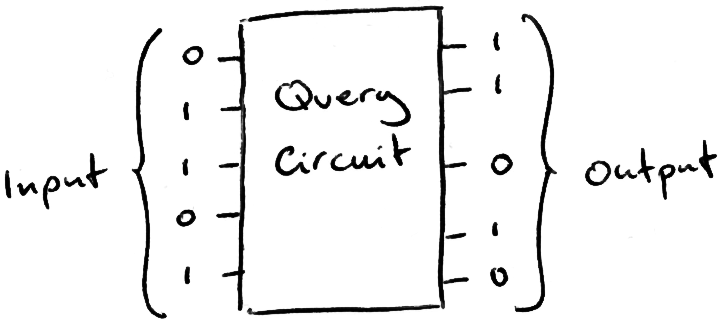
To perform a random guessing search, we input random addresses into the query circuit and check the output, repeating with different binary strings until the output equals the data we’re looking for. We add a ‘checker’ circuit that flips a ‘flag’ bit if our output is ω.
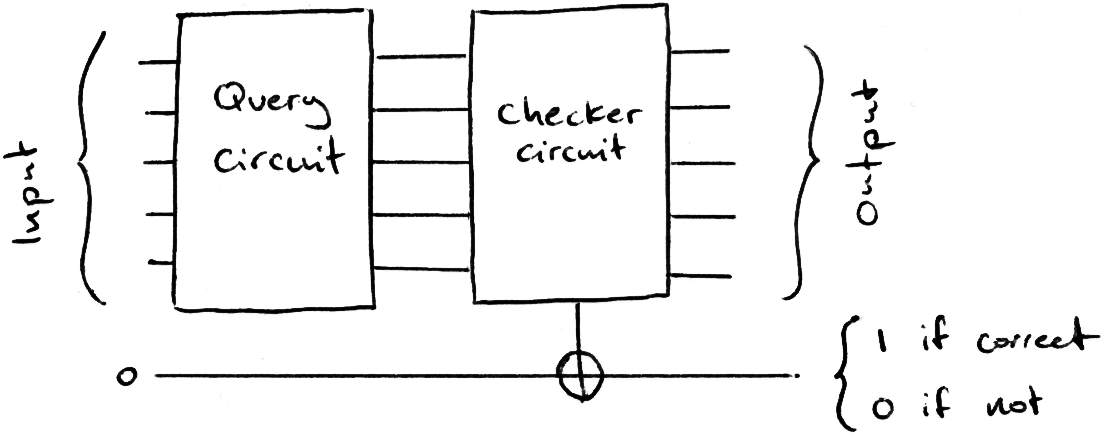
Using our phonebook analogy, we put random names into the query circuit until it outputs the phone number we were given. This algorithm has a complexity of order 2n (exponential time).