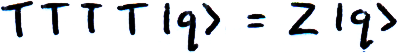Quantum Computing
Single Qubit Operations
In this section, we introduce quantum gates. Quantum gates are fundamental operations that act as building blocks for quantum algorithms. It can be shown that a small set of quantum gates is enough to carry out any quantum computation, we call these sets universal quantum gates. Understanding the operation of individual quantum gates is useful for demonstrating quantum phenomena and in turn understanding larger quantum algorithms.
Contents
The X, Y & Z-Gates
Single qubit quantum gates can be represented by a 2×2 matrix that acts on our 2D qubit vector. The X-gate is one such gate:
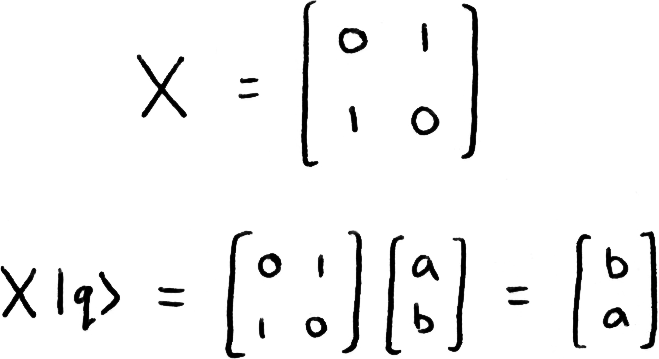
As we can see, the X-gate switches the amplitudes of |1⟩ and |0⟩ in our qubit, for this reason it is often known as a 'bit flip'. It is also analogous to the classical 'NOT' gate and similarly inherits this name as well.
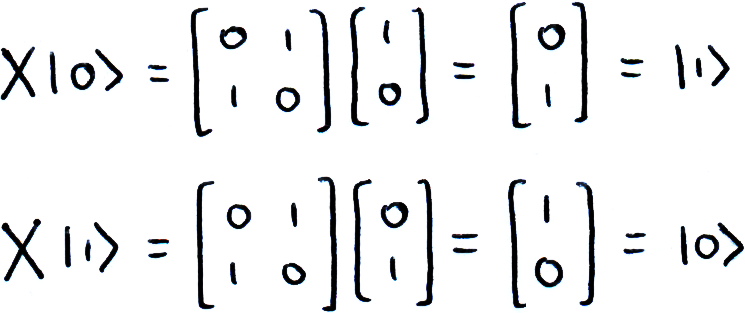
It is clear how to the X-gate operates on classical classical states, but what about on superpositions?

We can see that the X-gate has no effect on the state |+⟩, and introduces a negative phase to |-⟩, this is because these states are both eigenvectors of X.
The X-gate corresponds to a rotation of π around the X-axis of the Bloch sphere. Similarly the Y & Z-gates perform rotations of π around their respective axes:

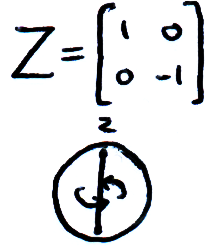
The H-Gate
The Hadamard gate (H-gate) has the matrix:

And creates superposition from a |0⟩ or |1⟩ state. As with the previous gates we've learnt about, the H-gate is its own inverse.
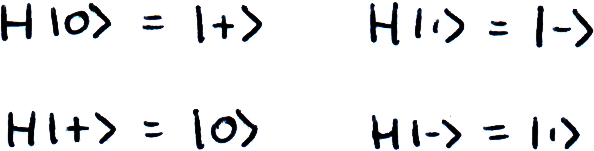
The Phase Shift Gate
The phase shift gate change the phase (surprise!) of the state |1⟩:
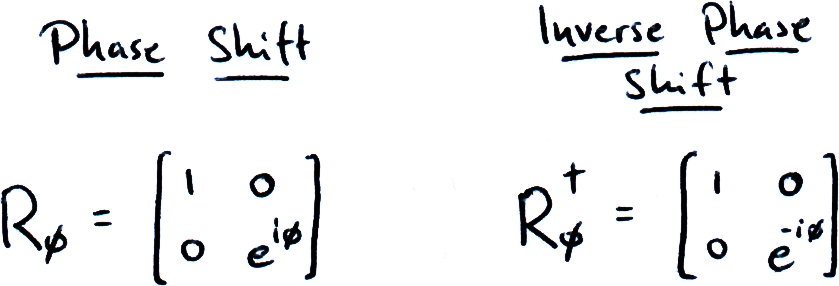
Unlike the previous gates, the phase shift gate is not necessarily its own inverse, to reverse the change we must apply a phase shift in the other direction. Theoretically we can choose any phase shift. We call the phase shift by ϕ = π/4 the T-gate:
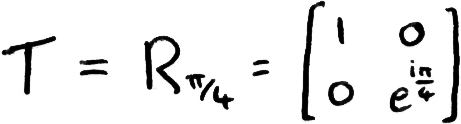
And we call the the phase shift by ϕ = π the Z-gate:

We can now see why the T-gate is sometimes known as the 4√ Z gate: because four successive T-gates have the same effect as one Z-gate.