The Deutsch-Joza Algorithm
How does the Deutsch-Joza algorithm work?
Lets look at the three main steps of the algorithm and try to work out what’s happening.
- Set the output qubit to |-⟩
- Apply H-gates to the input qubits
- Apply the black box
- Apply H-gates to the n input qubits
- Apply the black box
- Apply H-gates to the n input qubits
This is easily accomplished with a H-gate and a Z-gate.
Starting with the all-zeroes state (|000...0⟩), we apply a H-gate to each qubit. This puts each qubit into the state |+⟩, and we will call the new state of the register |s⟩. We can think of this state as an equal superposition of all the states in the computational basis:
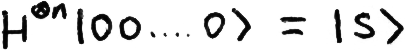
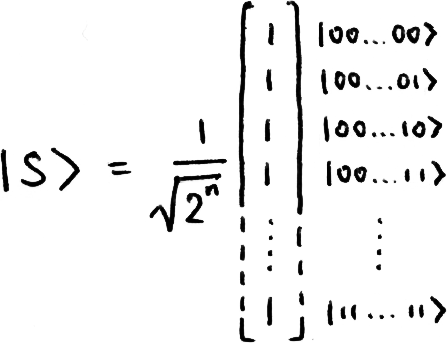
It’s important to remember for later in this explanation that H-gates are their own inverse, i.e. if we perform this operation on the state |s⟩, we will get back the state |00...0⟩ with certainty.
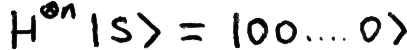
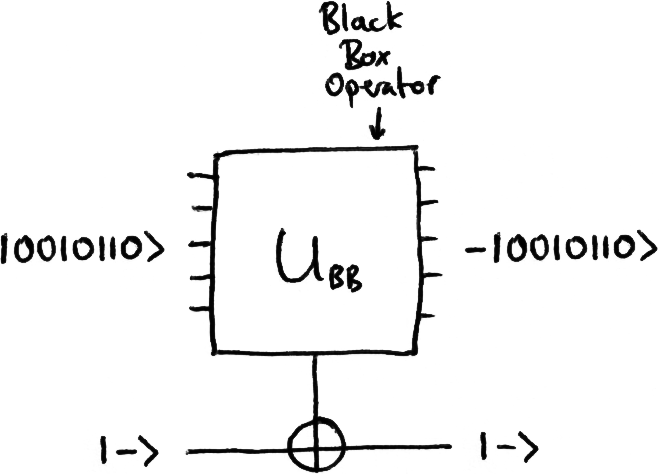
You may recall the Upside-Down CNOT circuit; the concepts there may help your understanding of this section.
If we feed the box a classical state, it can either do nothing, or it can trigger the box to flip the |-⟩ qubit. If a classical state does trigger the box to flip the |-⟩ qubit, this classical state inherits a negative phase:
At this point, our explanation branches into two separate cases, the case of the constant box and the case of the balanced box. Let’s start with the constant box:
Constant Box
Since our box is constant, the X-gate at the bottom of our circuit is either triggered for every classical input, or for none. When we pass our black box the state |s⟩, we are guaranteed to either get all our states back untouched, or all with a negative phase:
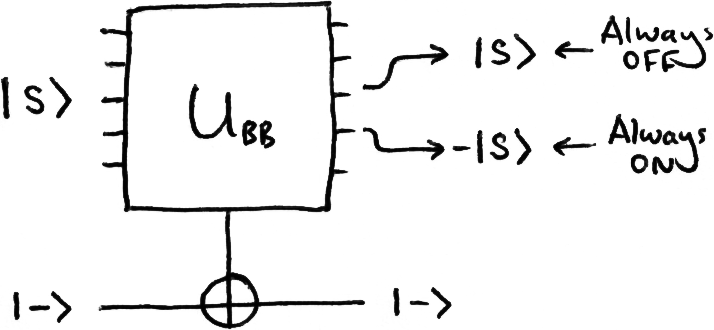
We see that the probability of measuring the state |s⟩ is exactly 1 for both types of constant box:
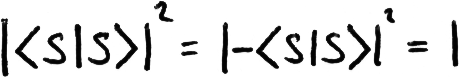
This is a good demonstration of global phase being ignored. The states |s⟩|-⟩ and -|s⟩|-⟩ are completely equivalent to us.
As mentioned before, this step transforms the state |s⟩ into the state |000...0⟩. Since we were left with either |s⟩ or -|s⟩ from the previous step, we will be left to measure either |000...0⟩ or -|000..0⟩, which gives us a 100% chance of measuring each qubit in the state |0⟩.
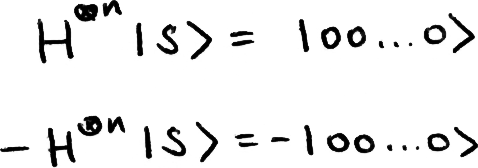
Balanced Box
Since our box is balanced, the X-gate at the bottom of our circuit is triggered for exactly half the classical inputs. This means we’re going to get back a superposition that looks something like this:
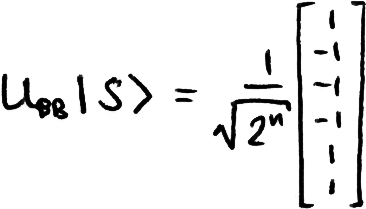
We can see that this new state vector is perpendicular to |s⟩, so the probability that we find our system in the state |s⟩ is exactly 0.
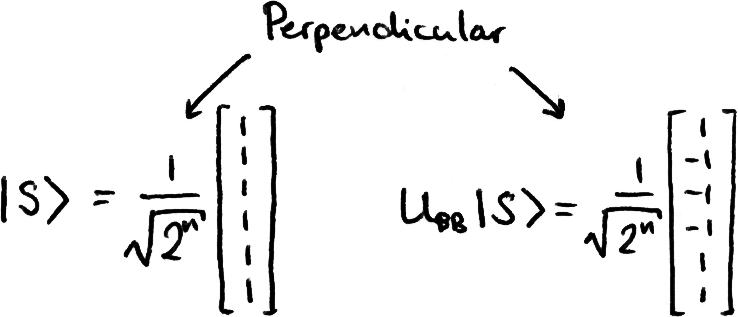
As mentioned before, this operation transforms the state |s⟩ into the state |000...0⟩. Since we were left with a state perpendicular to |s⟩, after this final transformation we’re going to end up with a state perpendicular to |000...0⟩, therefore the probability of measuring all qubits |0⟩ is exactly 0.
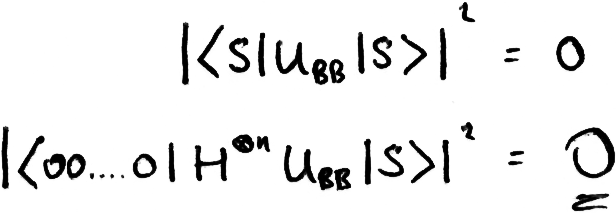
Summary
In this section you’ve seen some different notations and ways of thinking used in action, you’ve seen some basic quantum computing principles at work, and you’ve understood an example of an algorithm a quantum computer can perform better than a conventional computer. Almost all of the individual techniques and processes here are reused in some form or another in larger, more exciting algorithms.
To consolidate this, I highly recommend working through the maths independently with a pen and paper, and experimenting with simulations in Quirk.