Preliminary Mathematics
Vectors and Matrices in Quantum Computing
In this section we revise properties of matrices and vectors. We use informal definitions for the purposes of this site, so some of the statements in this section are true only for the scenarios we encounter in quantum computing and not for mathematics in general.
Contents
Orthonormal Bases
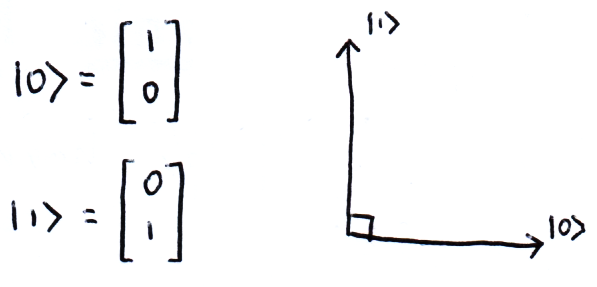
Two vectors are orthogonal if their inner product is zero. A vector is normalised if its magnitude is one. Orthonormal vectors are both orthogonal and normalised. In quantum computing we use the orthonormal basis vectors |0⟩ and |1⟩ to represent the off and on states of our qubits:
These are not the only bases we will come across. The other most common 2D basis in quantum computing is made from the vectors |+⟩ & |-⟩:
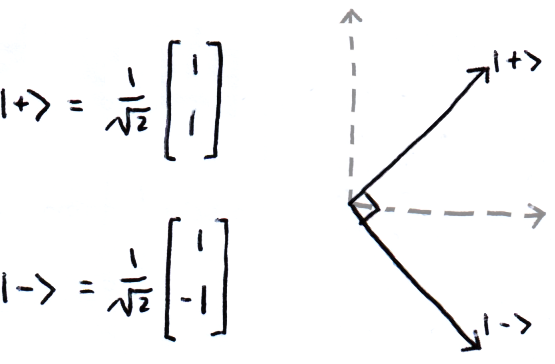
We can also write these in terms of |0⟩ and |1⟩, and we can easily see what their inner products will give:
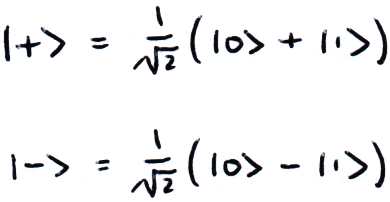
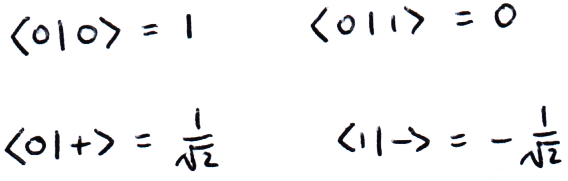
There is also the basis made from |↻⟩ and |↺⟩, although this is less commonly used:
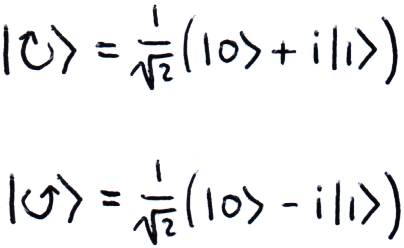
The Conjugate Transpose
The conjugate transpose, also known as the Hermitian transpose, means taking the transpose of the matrix and complex conjugate of each element. In quantum computing we denote the conjugate transpose with a dagger (†):
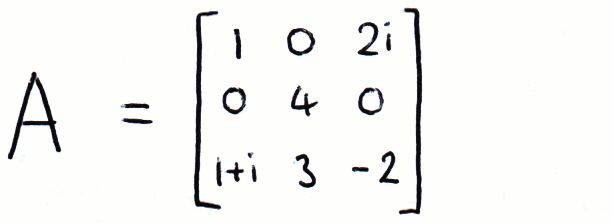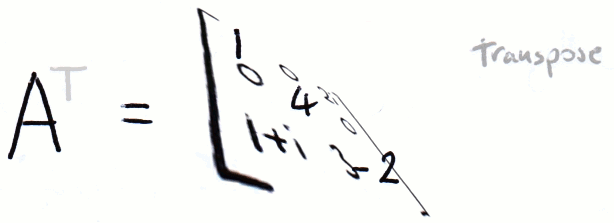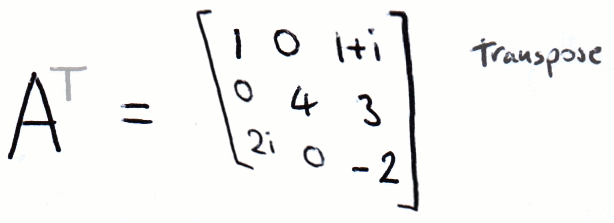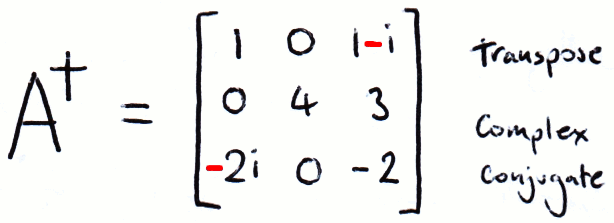
Unitary Matrices
A matrix is unitary if it’s conjugate transpose is its inverse:

We can see that any matrix formed from the product of two unitary matrices is also unitary:
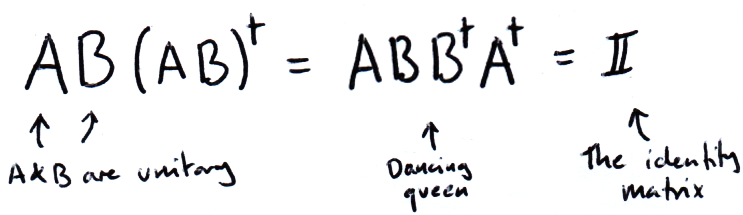
Hermitian Matrices
A Hermitian matrix is a matrix that is equal to its conjugate transpose:
