Preliminary Mathematics

Index Next

Dirac Notation and Basic Matrix Algebra

Here we introduce Dirac notation and revise some basic matrix algebra in the process.

Bras & Kets
The Inner Product
The Outer Product
The Kronecker Product

Bras & Kets

In matrix algebra, we have row and column vectors, in Dirac notation we write these vectors as ⟨Bras| and |Kets⟩ respectively. When bras, kets or matrices are next to eachother, matrix multiplication is implied. The advantage of this notation will become clear as we progress through the section.

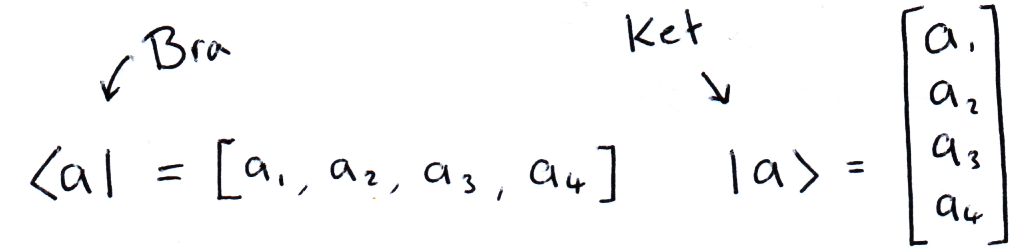
A 'bra' represents a row vector (left) and a 'ket' represents a column vector

The Inner Product

If we multiply a bra and a ket using matrix multiplication, we get a scalar quantity (for simplicity we regard complex numbers as scalars):

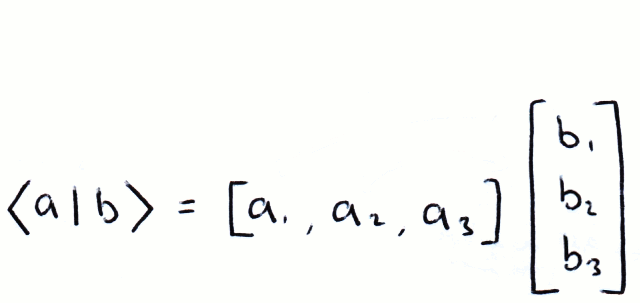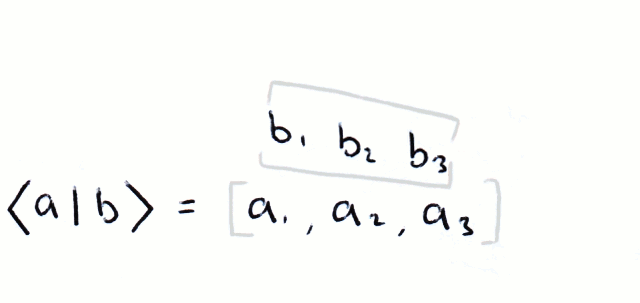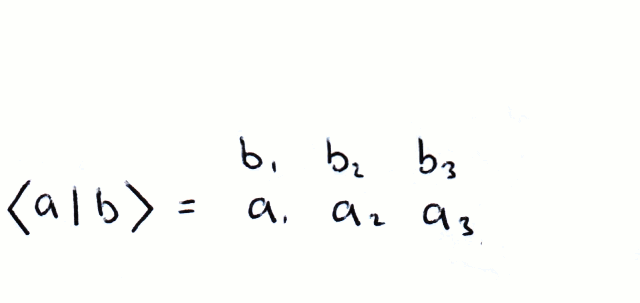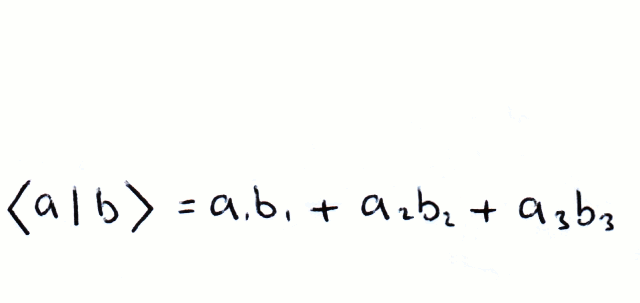
This is called the inner product. If |a⟩ and |b⟩ are orthogonal then:

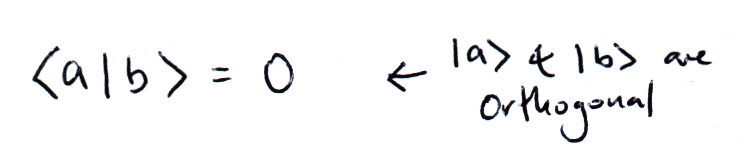
If two vectors are orthogonal, their inner product will be 0.

And if |a⟩ is normalised then:

Normalised vectors have a magnitude of 1

We can describe another vector as a combination of vectors. It's easy to see that if we can write a vector in terms of a convenient basis, certain multiplications become simpler. In this example, |a⟩ and |b⟩ are orthogonal:

We can write vectors as linear combinations of other vectors

An example of calculating the inner product, where |a⟩ & |b⟩ are orthogonal

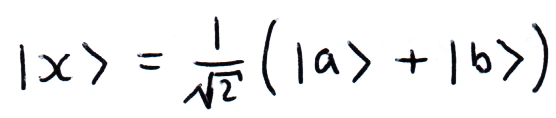
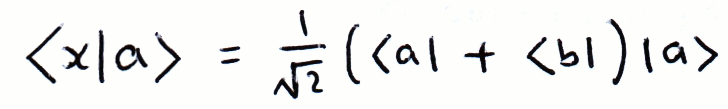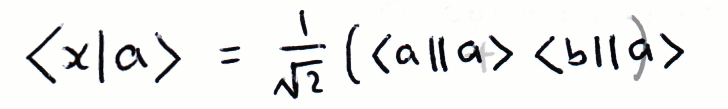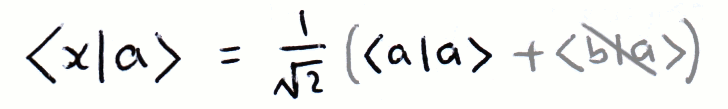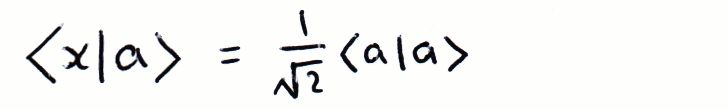
The Outer Product

Again, following the rules of matrix multiplication, we can compute the outer product using a ket and a bra:

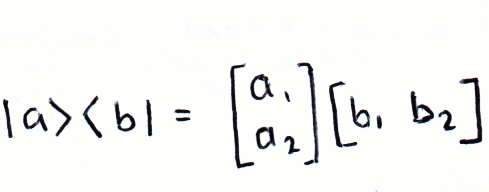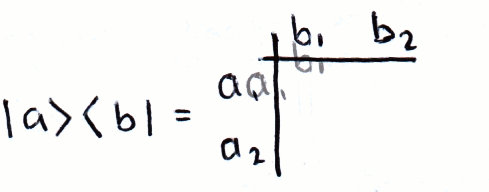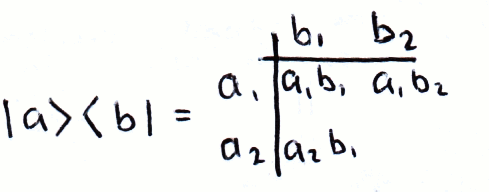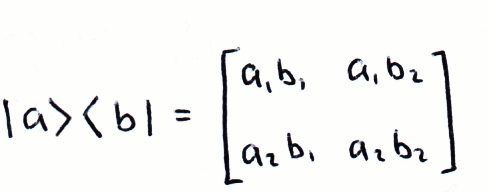
We can write matrices in this form, for example:

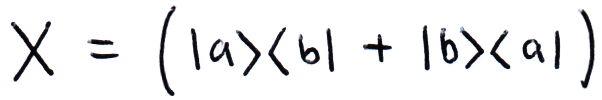
If we write matrices in this way, it becomes clear what the result of multiplication will be, even if we don't know what its elements are. For example, if |a⟩ and |b⟩ are orthonormal:

An example multiplication of a matrix, X, with a vector, |a⟩, where |a⟩ & |b⟩ are orthonormal

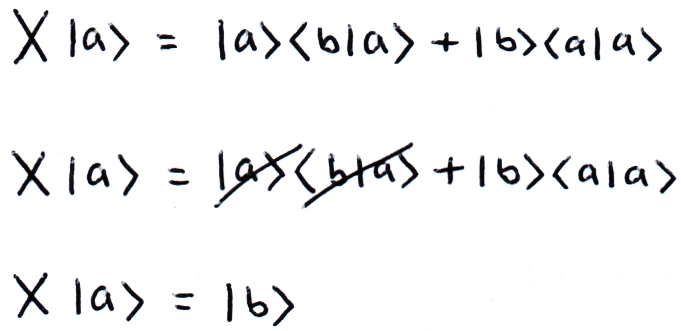
The Kronecker Product

We can also multiply using the Kronecker product:

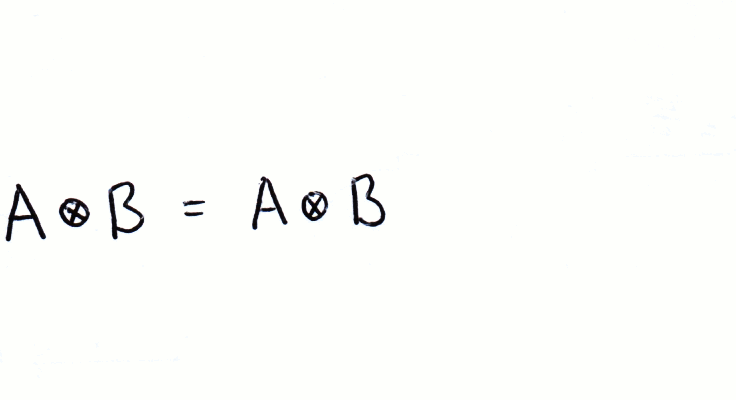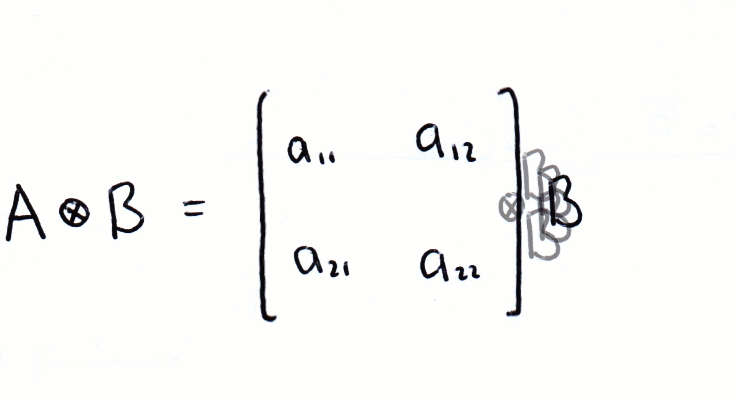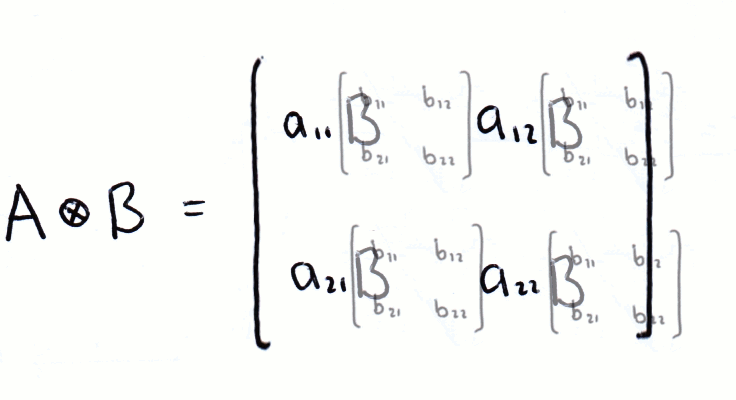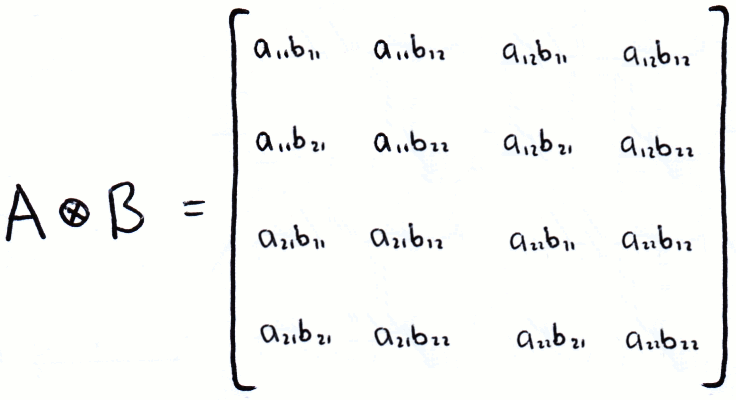
As you can see in the image above, the Kronecker product is notated by a circle with a cross in it (⊗). Often the kronecker product is implied when writing two kets next to eachother, i.e. |a⟩|b⟩ = |a⟩⊗|b⟩.

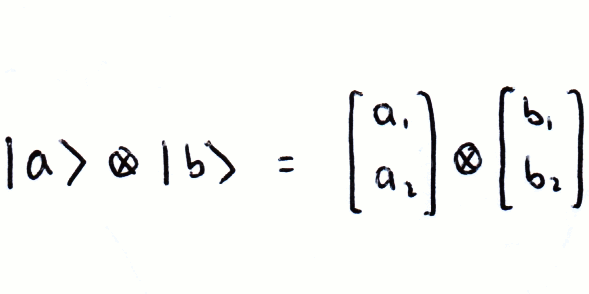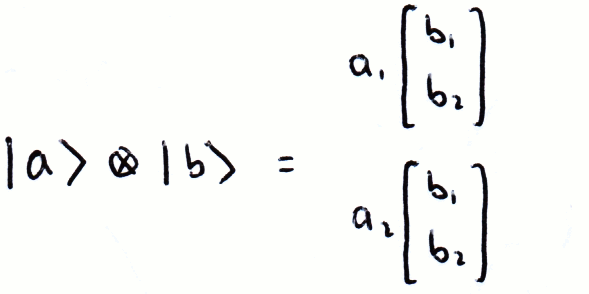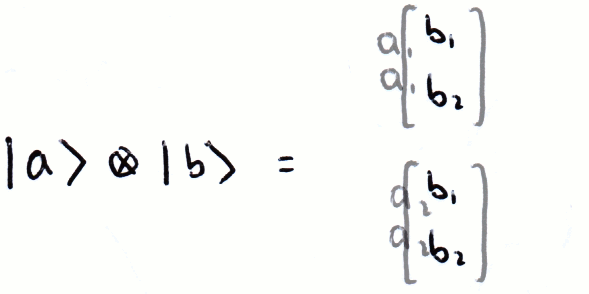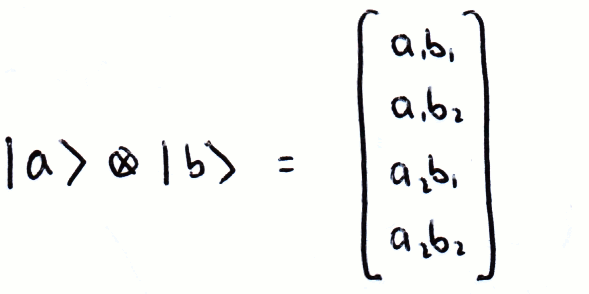
Multiplying two 2D vectors with the Kronecker product

Fortunately in this site we only consider square matrices and finite vectors with 2ⁿ elements, this simplifies a lot of algebra. In quantum computing we describe our computer's state through vectors, using the Kronecker product very quickly creates large matrices with many elements and this exponential increase in elements is where the difficulty in simulating a quantum computer comes from. We will discuss this properly in (link to section).